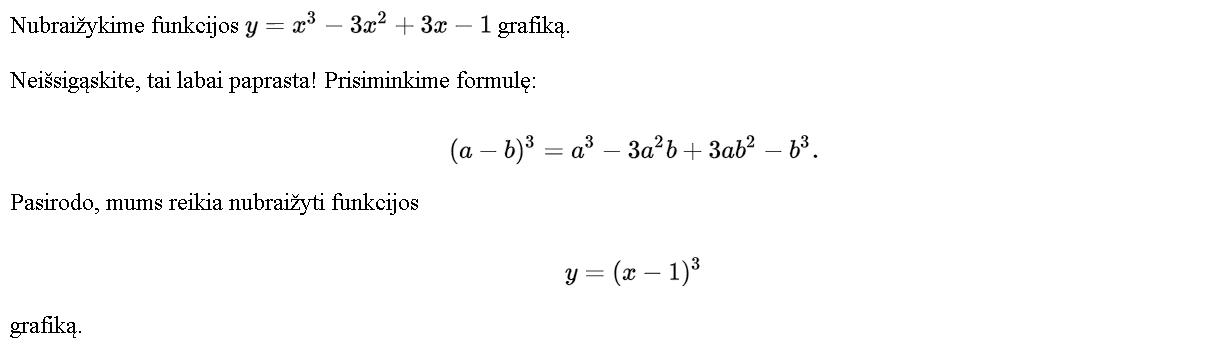Laipsninė funkcija

1

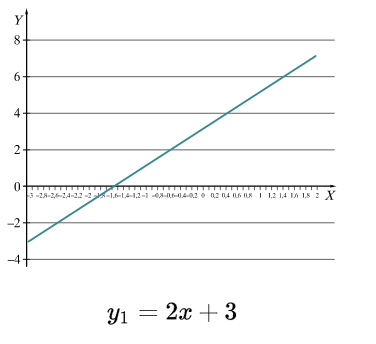
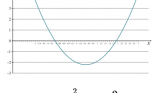
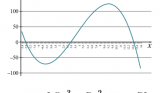
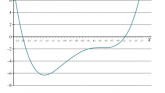
Laipsninių daugianarių funkcijos

Paaiškinama, kas yra laipsninės funkcijos. MO 1 kadras.

Parodoma, kokie įvairūs laipsninių daugianarių funkcijų grafikai.

2

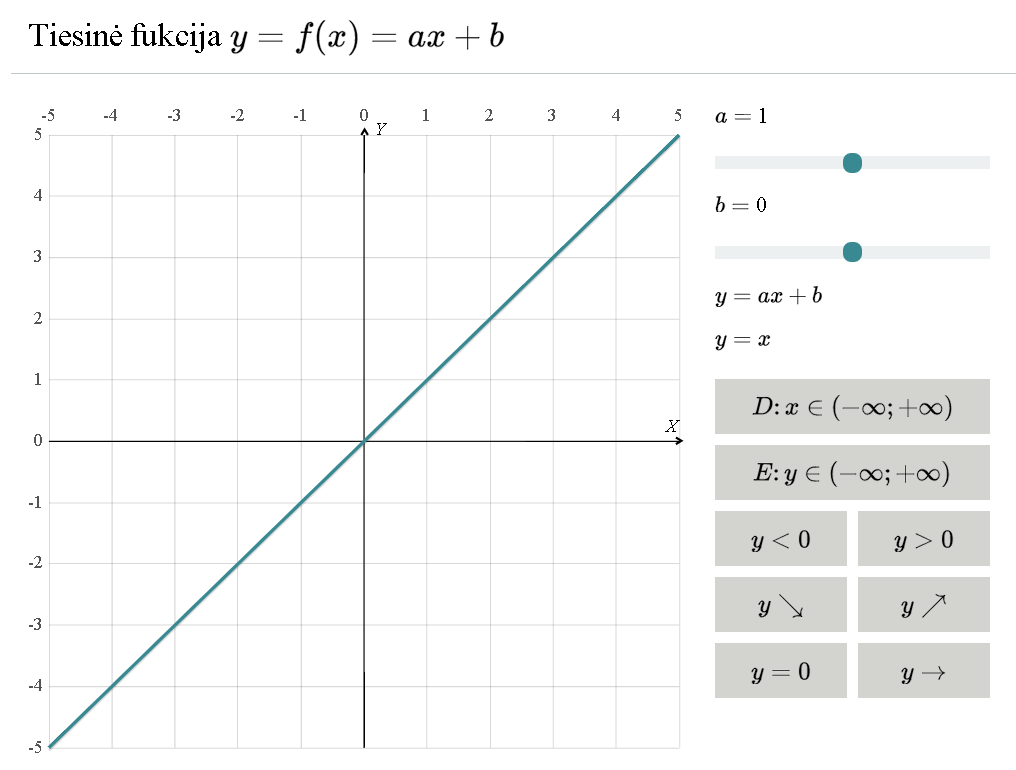
Pirmo laipsnio funkcija

Nuosekliai dinaminiu paveikslėliu primenami pirmojo laipsnio funkcijos grafikai: horizontali tiesė; vertikali tiesė; neigiamas krypties koeficientas; teigiamas krypties koeficientas; koeficiento b prasmė. MO 2 epizodas.

3

Užduotis

Naudojamasi SMP įrankiu. 1/12 Tiesinė funkcija.

Aukštesnysis lygis
  • Sumodeliuokite tiesę [latex]y_2 = a_2x + b_2[/latex], einančią per taškus: [latex]A(0;-2)[/latex] ir [latex]B(1;3)[/latex], ir užrašykite jos krypties koeficiento reikšmę.
  • Naudodamiesi įrankiu, užrašykite pagrindines savybes (apibrėžimo ir reikšmių sritis; teigiamas, neigiamas reikšmes; didėjimo, mažėjimo intervalus; funkcijos nulius).
  • Taškai [latex]M(2;y)[/latex] ir [latex]N(x,4)[/latex] priklauso tiesei [latex]y_2[/latex]. Apskaičiuokite [latex]x[/latex] ir [latex]y[/latex] reikšmes.
  • Užrašykite tiesę [latex]y_3 = a_{3}x + b_3[/latex], kuri būtų lygiagreti tiesei [latex]y_2[/latex] ir eitų per tašką [latex]C(-1;3)[/latex].
  • Užrašykite tiesę [latex]y_4 = a_{4}x + b_4[/latex], kuri būtų statmena tiesei [latex]y_2[/latex] ir eitų per tašką [latex]D(0;2)[/latex].

Pagrindinis lygis
  • Sumodeliuokite tiesę [latex]y_2 = a_2x + b_2[/latex], einančią per taškus: [latex]A(0;-2)[/latex] ir [latex]B(1;3)[/latex], ir užrašykite jos krypties koeficiento reikšmę.
  • Naudodamiesi įrankiu, užrašykite pagrindines savybes (apibrėžimo ir reikšmių sritis; teigiamas, neigiamas reikšmes; didėjimo, mažėjimo intervalus; funkcijos nulius).
  • Taškai [latex]M(2;y)[/latex] ir [latex]N(x,4)[/latex] priklauso tiesei [latex]y_2[/latex]. Apskaičiuokite [latex]x[/latex] ir [latex]y[/latex] reikšmes.
  • Užrašykite tiesę [latex]y_3 = a_{3}x + b_3[/latex], kuri būtų lygiagreti tiesei [latex]y_2[/latex] ir eitų per tašką [latex]C(-1;3)[/latex].

Patenkinamas lygis
  • Sumodeliuokite tiesę [latex]y_2 = a_2x + b_2[/latex], einančią per taškus: [latex]A(0;-2)[/latex] ir [latex]B(1;3)[/latex], ir užrašykite jos krypties koeficiento reikšmę.
  • Naudodamiesi įrankiu, užrašykite pagrindines savybes (apibrėžimo ir reikšmių sritis; teigiamas, neigiamas reikšmes; didėjimo, mažėjimo intervalus; funkcijos nulius).
  • Taškai [latex]M(2;y)[/latex] ir [latex]N(x,4)[/latex] priklauso tiesei [latex]y_2[/latex]. Apskaičiuokite [latex]x[/latex] ir [latex]y[/latex] reikšmes.

4

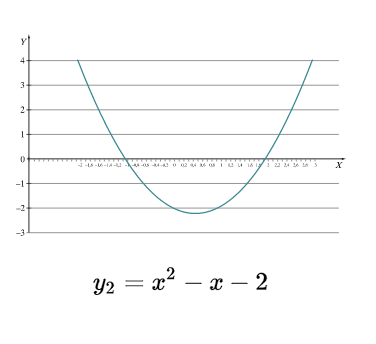
Kvadratinė funkcija

Vaizdo įrašu primenama apie kvadratinio trinario funkcijas ir grafiką – parabolę (MO 3 epizodas).

Vaizdo įrašu paaiškinama, kas yra parabolė (MO 4 epizodas).

Demonstruojama Parabola animacija. Mokytojo komentarai.

Primenamos trys skirtingos parabolės formos. Demonstruojamas dinaminės matematikos programos Geogebra įrankis.

5

Užduotis

Naudojamasi SMP įrankiu. 2/12 Kvadratinė funkcija.

Aukštesnysis lygis
  • Sumodeliuokite parabolę [latex]y_1 = ax^2 + bx + c[/latex], einančią per taškus [latex]A(0;0)[/latex], [latex]B(4;0)[/latex] ir [latex]C(2;4)[/latex], ir užrašykite koeficientų [latex]a,b,c[/latex] reikšmes.
  • Naudodamiesi įrankiu, užrašykite pagrindines savybes (apibrėžimo ir reikšmių sritis; teigiamas, neigiamas reikšmes; didėjimo, mažėjimo intervalus; funkcijos nulius; didžiausią, mažiausią reikšmes).
  • Taškai [latex]M(1;y)[/latex] ir [latex]N(x;-5)[/latex] priklauso parabolei [latex]y_1[/latex]. Apskaičiuokite [latex]x[/latex] ir [latex]y[/latex] reikšmes.
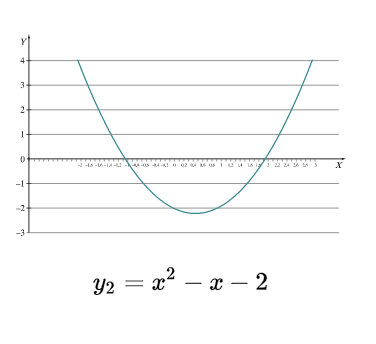
  • Sumodeliuokite ir užrašykite parabolę [latex]y_2[/latex], kurios viršūnė taške [latex]V(2;2)[/latex], ir kuri eina per tašką [latex]D(0;4)[/latex].

Pagrindinis lygis
  • Sumodeliuokite parabolę [latex]y_1 = ax^2 + bx + c[/latex], einančią per taškus [latex]A(0;0)[/latex], [latex]B(4;0)[/latex] ir [latex]C(2;4)[/latex], ir užrašykite koeficientų [latex]a,b,c[/latex] reikšmes.
  • Naudodamiesi įrankiu, užrašykite pagrindines savybes (apibrėžimo ir reikšmių sritis; teigiamas, neigiamas reikšmes; didėjimo, mažėjimo intervalus; funkcijos nulius; didžiausią, mažiausią reikšmes).
  • Taškai [latex]M(1;y)[/latex] ir [latex]N(x;-5)[/latex] priklauso parabolei [latex]y_1[/latex]. Apskaičiuokite [latex]x[/latex] ir [latex]y[/latex] reikšmes.

Patenkinamas lygis
  • Sumodeliuokite parabolę [latex]y_1 = ax^2 + bx + c[/latex], einančią per taškus [latex]A(0;0)[/latex], [latex]B(4;0)[/latex] ir [latex]C(2;4)[/latex], ir užrašykite koeficientų [latex]a,b,c[/latex] reikšmes.
  • Naudodamiesi įrankiu, užrašykite pagrindines savybes (apibrėžimo ir reikšmių sritis; teigiamas, neigiamas reikšmes; didėjimo, mažėjimo intervalus; funkcijos nulius; didžiausią, mažiausią reikšmes).

6

Namų darbai. Nr. 1

Pateikiama užduotis naudojantis Geogebra įrankiu.
Ūkininkas turi 24 metrus tvoros ir nori atitverti stačiakampio formos sklypelį. Viena sklypo briauna bus tvarto siena (raudona linija).

Aukštesnysis lygis
  • Tvoros ilgį (fencing) nustatykite 24 ir keisdami stačiakampio kraštinę stebėkite ploto ([latex]P[/latex]) reikšmių kitimą. Kokią kreivę piešia taškas [latex]P[/latex], judėdamas koordinačių plokštumoje?
  • Vieną stačiakampio kraštinę pažymėję [latex]x[/latex], parodykite, kad ploto funkcija [latex]y = P(x) = -2x^2 +24x[/latex].
  • Nubrėžkite ploto priklausomybės nuo kraštinės ilgio grafiką.
  • Palyginkite [latex]P(8)[/latex] ir [latex]P(4)[/latex].
  • Apskaičiuokite didžiausią sklypo plotą, kurį gali atsitverti ūkininkas.
  • Kokio ilgio tvoros reikėtų ūkininkui, kad taip aptvertų 100 kvadratinių metrų plotą?

Pagrindinis lygis
  • Tvoros ilgį (fencing) nustatykite 24 ir keisdami stačiakampio kraštinę stebėkite ploto ([latex]P[/latex]) reikšmių kitimą. Kokią kreivę piešia taškas [latex]P[/latex] judėdamas koordinačių plokštumoje?
  • Vieną stačiakampio kraštinę pažymėję [latex]x[/latex], parodykite, kad ploto funkcija [latex]y = P(x) = -2x^2 +24x[/latex].
  • Nubrėžkite ploto priklausomybės nuo kraštinės ilgio grafiką.
  • Palyginkite [latex]P(8)[/latex] ir [latex]P(4)[/latex].

Patenkinamas lygis
  • Tvoros ilgį (fencing) nustatykite 24 ir keisdami stačiakampio kraštinę stebėkite ploto ([latex]P[/latex]) reikšmių kitimą. Kokią kreivę piešia taškas [latex]P[/latex] judėdamas koordinačių plokštumoje?
  • Nubrėžkite ploto priklausomybės nuo kraštinės ilgio grafiką.
  • Palyginkite [latex]P(8)[/latex] ir [latex]P(4)[/latex].

7

Namų darbai. Nr. 2

Įjungus parabolės formą, priklausomai nuo to, kaip ši apibrėžiama, galime judinti koeficientus, viršūnę ar šakas. Ar pavyktų visas jas sustumti taip, kad visos eitų per tašką (0,3), o viršūnė atsidurtų taške (1,1)? Atsakymą pagrįskite.

8

Antra pamoka

Patikrinami namų darbai. Mokytojo komentarai. Vertinimas.

9

Lyginės ir nelyginės funkcijos

Vaizdžiai ir paprastai paaiškinama apie lygines ir nelygines funkcijas (MO 5 epizodas).

Akcentuojama: jeigu [latex]f(-x) = f(x)[/latex], tai funkcija yra lyginė, jeigu [latex]f(-x) = -f(x)[/latex], tai funkcija nelyginė, o jeigu [latex]f(-x) = g(x)[/latex], tai funkcija nei lyginė, nei nelyginė.

Pateikiama užduotis patikrinti pateiktų funkcijų lyginumą. [latex]f(x) = x^2; g(x) = x^2 + x; k(x) = x^3 + x[/latex]

10

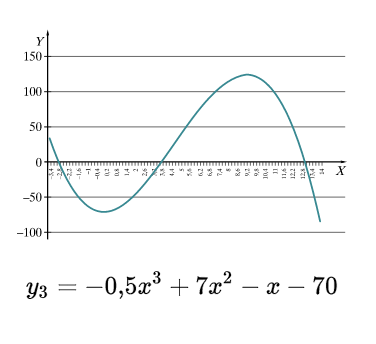
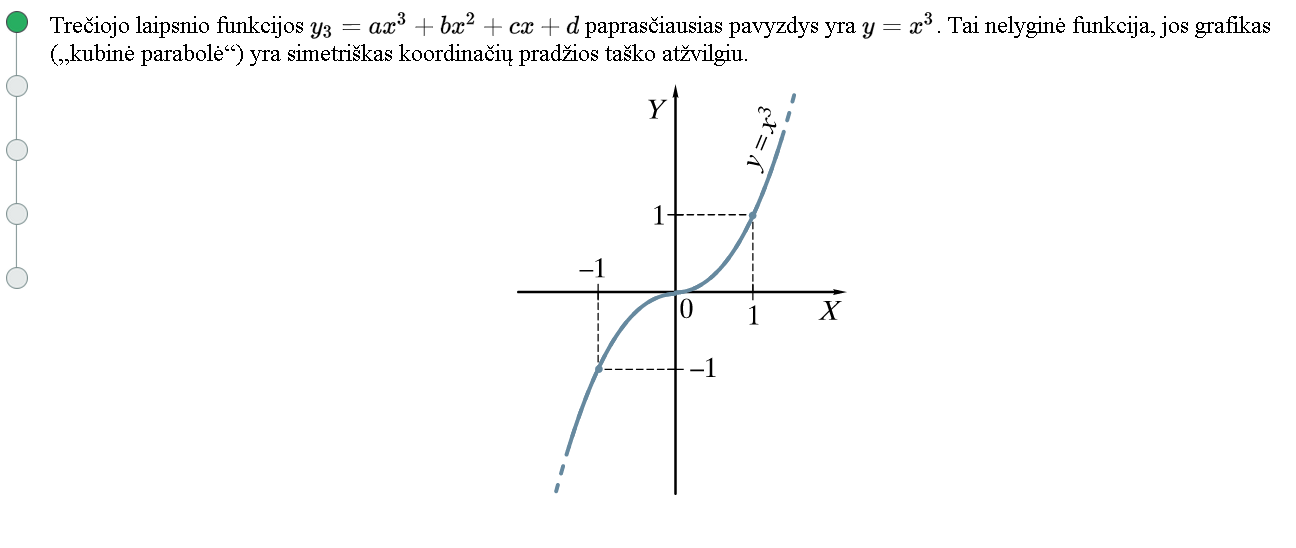
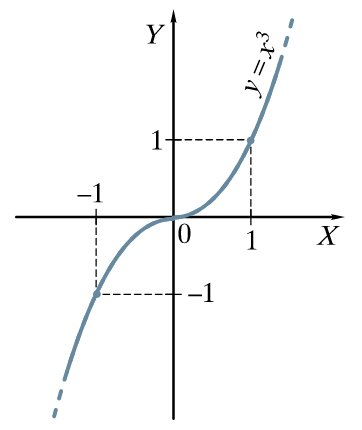
Kubinės funkcijos grafikas

Demonstruojama, kaip pertvarkomas reiškinys [latex]x^3 – 3 x^2 + 3x -1[/latex] pasinaudojant greitos daugybos taisykle [latex](a-b)^3 = a^3 -3a^{2}b + 3ab^2 -b^3[/latex].

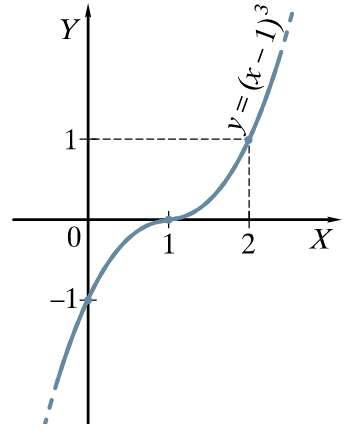
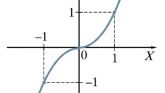
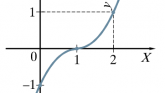
Demonstruojama, kaip nubraižomas funkcijos [latex]y = x^3 – 3 x^2 + 3x -1 = (x-1)^3[/latex] grafikas, ir paaiškinama apie grafiko transformaciją Ox ašimi.

11

Užduotis

Mokiniai naudojasi dinaminės geometrijos Geogebra įrankiu.

  • Uždėjus varnelę ant [latex]f(x) = ax^3[/latex], matomas raudonas grafikas. Mokinių prašoma paaiškinti, kaip keičiasi kubinės parabolės grafikas, slankjuostėje keičiant skaičiaus [latex]a[/latex] reikšmę. Akcentuojama, kai [latex]a>0[/latex] ir [latex]a<0[/latex].
  • Uždėjus varnelę ant [latex]g(x) = x^3 + c[/latex], matomas mėlynas grafikas ir paliekamas raudonas [latex]f(x) = 1 \cdot x^3[/latex] grafikas. Mokinių prašoma paaiškinti, kaip keičiasi kubinės parabolės grafikas, slankjuostėje keičiant skaičiaus [latex]c[/latex] reikšmę. Akcentuojama, jog grafiko forma nesikeičia, jis tik pastumiamas [latex]O_y[/latex] ašimi aukštyn, jeigu [latex]c>0[/latex], ir stumiamas žemyn, jeigu [latex]c<0[/latex].
  • Uždėjus varnelę ant [latex]h(x) = (x+b)^3[/latex], matomas žalias grafikas ir paliekamas raudonas [latex]f(x)=1 \cdot x^3[/latex] grafikas. Mokinių prašoma paaiškinti, kaip keičiasi kubinės parabolės grafikas, slankjuostėje keičiant skaičiaus [latex]b[/latex] reikšmę. Akcentuojama, jog grafiko forma nesikeičia, jis tik pastumiamas [latex]O_x[/latex] ašimi kairėn, jeigu [latex]c>0[/latex], ir stumiamas dešinėn, jeigu [latex]c<0[/latex].
  • Mokinių klausiama, kaip, turint funkcijos [latex]f(x) = ax^3[/latex] grafiką, galima nubrėžti funkcijos [latex]k(x) = a(x+b)^3 + c[/latex] grafiką. Akcentuojama transformacijos [latex]O_y[/latex] ir [latex]O_x[/latex] ašimis.

12

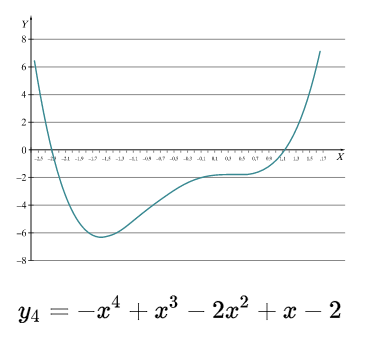
Ketvirtojo, penktojo ir aukštesnių laipsnių funkcijos

Trumpai komentuojamos ketvirtojo, penktojo ir aukštesnių laipsnių funkcijos.

13

Daugianarių skaidymas

Vaizdo įrašu parodoma, kaip skaidyti daugianarius.

14

Užduotis

Mokinių prašoma, naudojantis Lyginio laipsnio funkcija (SMP įrankis 3/12) ir Nelyginio laipsnio funkcija (SMP įrankis 4/12), patyrinėti šių funkcijų grafikus. Mokytojo ir mokinių diskusija.

15

Užduotis

Rinkinio pabaigoje pateikiamos trijų sudėtingumo lygių trumpo atsakymo užduotys.

Aukštesnysis lygis

Mokiniams rekomenduojamos A lygio užduotys.

Pagrindinis lygis

Mokiniams rekomenduojamos A lygio užduotys.

Patenkinamas lygis

Mokiniams rekomenduojamos B lygio užduotys.

16

Motyvuojantis intarpas

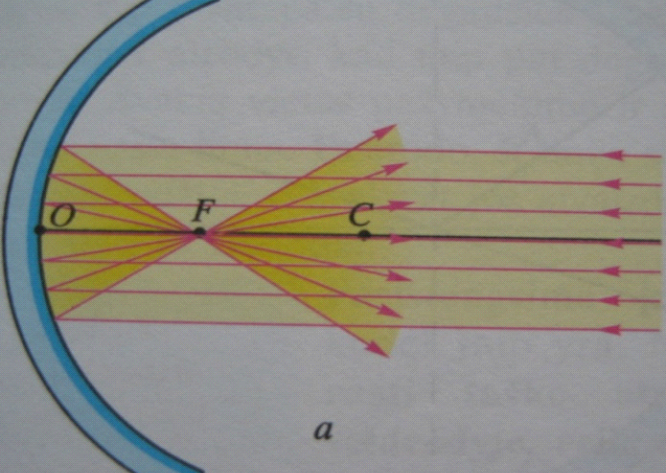
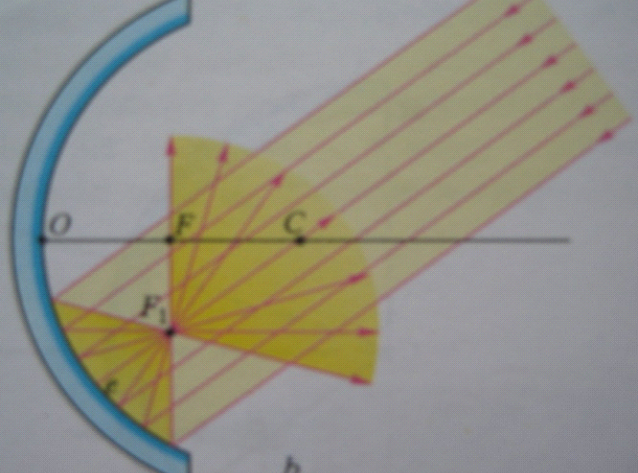
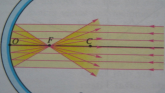
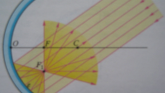
Paraboliniai veidrožiai. Jeigu į įgaubtą veidrodį nukreipsime pluoštą lygiagrečių pagrindinei ašiai spindulių, tai visi atsispindėję spinduliai eis per pagrindinės optinės ašies tašką F, vadinamą pagrindiniu veidrodžio židiniu. OF – pagrindinis židinio nuotolis. Įgaubti veidrodžiai yra glaudžiamieji. Iškilieji veidrodžiai yra sklaidomieji, nuo jų atsispindėję spinduliai išsklaidomi.

17

Namų darbai. Nr. 3

Aprašomas originalus būdas programinėmis priemonėmis „pamatyti“ grafiką nuliui artimoje aplinkoje (MO 7 epizodas).

18

Namų darbai. Nr. 4

Rinkinio pabaigoje pateikiamos trijų sudėtingumo lygių pasirenkamojo atsakymo užduotys.

Aukštesnysis lygis

Mokiniams rekomenduojamos A lygio užduotys.

Pagrindinis lygis

Mokiniams rekomenduojamos A lygio užduotys.

Patenkinamas lygis

Mokiniams rekomenduojamos B lygio užduotys.

19

Motyvuojantis namų darbas

Siūloma paskaityti Parabolinė antena – puikiausias saulės kolektorius ir Saulės energiją vartojantis žiebtuvėlis (vaizdo medžiaga).

Mokiniams siūloma technologijų pamokose pasigaminti naudingų daiktų iš nebrangių medžiagų.

20

Pasiekimų ir pažangos vertinimas

Pamokoje naudojamas kaupiamasis vertinimas, kuris taikomas vertinant:

  • teisingus mokinių atsakymus į klausimus;
  • savarankiško darbo užduotis;
  • mokėjimą pagrįsti išsakytą nuomonę;
  • aktyvumą ir iniciatyvumą pamokoje;
  • pagalbą draugui;
  • mokymosi pažangą.

Namų darbų užduotis pristatoma ir aptariama kitos pamokos pradžioje. Išsamiausi atsakymai ir pristatymai vertinami kaupiamaisiais balais.

21

Apibendrinimas

Pamokos refleksijai skiriamos kelios minutės. Mokiniai peržvelgia savo užrašus, prisimena veiklas ir pildo pasiūlytą lentelę.

 
Nesupratau
 
Reikia
pasigilinti
 
Žinau, supratau,
galiu
 

Mokytojas paprašo perskaityti savo refleksijas, trumpai pakomentuoja jas, patardamas, kaip ir į ką turėtų atkreipti dėmesį mokiniai, siekdami geresnių rezultatų.