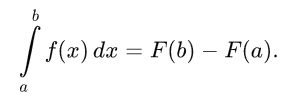1
Temos probleminė užduotis
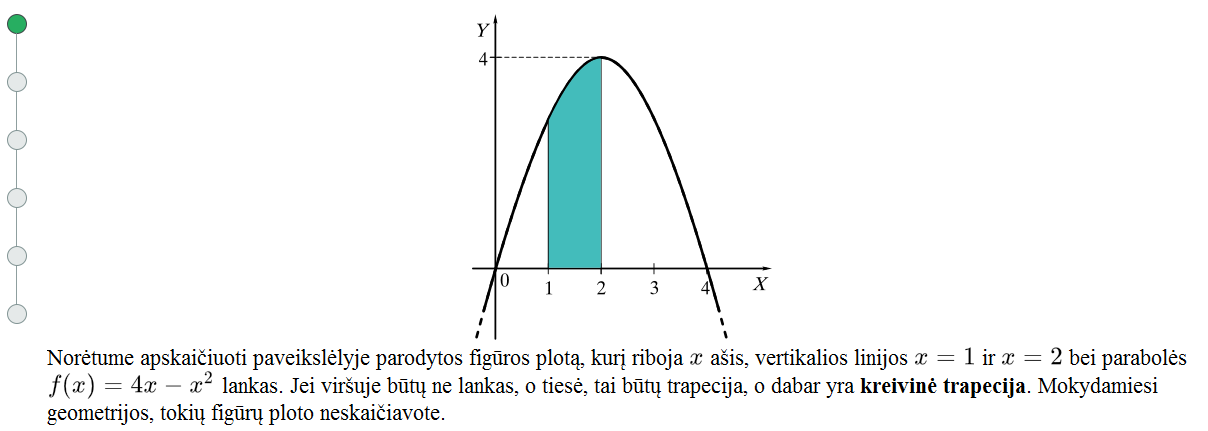
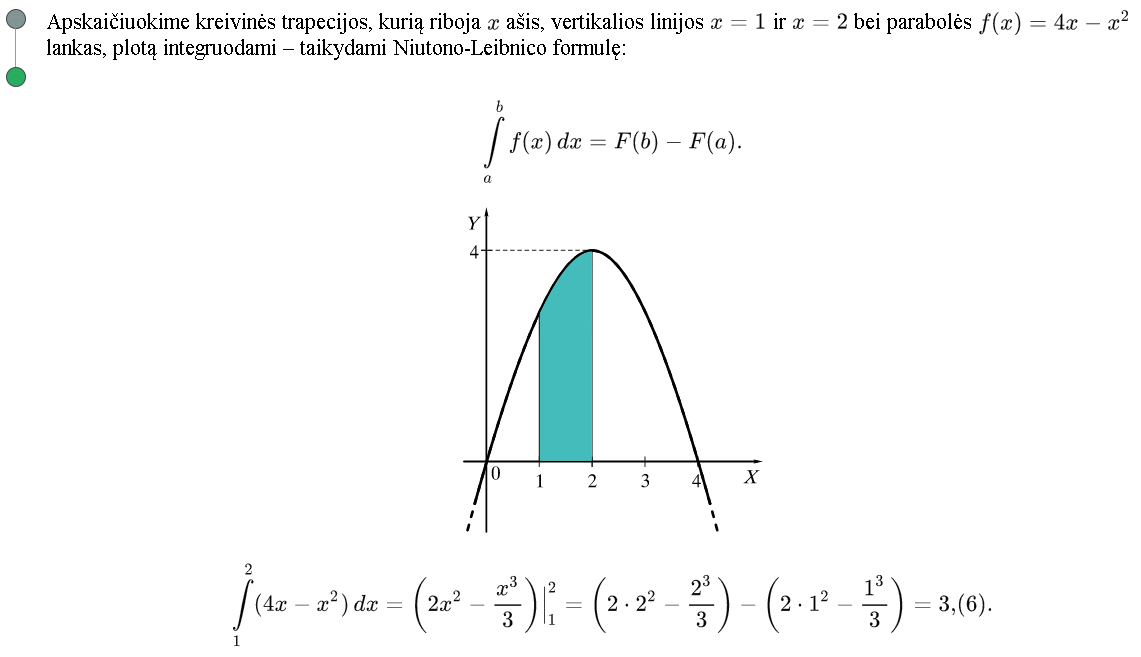
Apskaičiuoti paveikslėlyje parodytos figūros plotą. Apibrėžiama, ką vadiname kreivine trapecija.
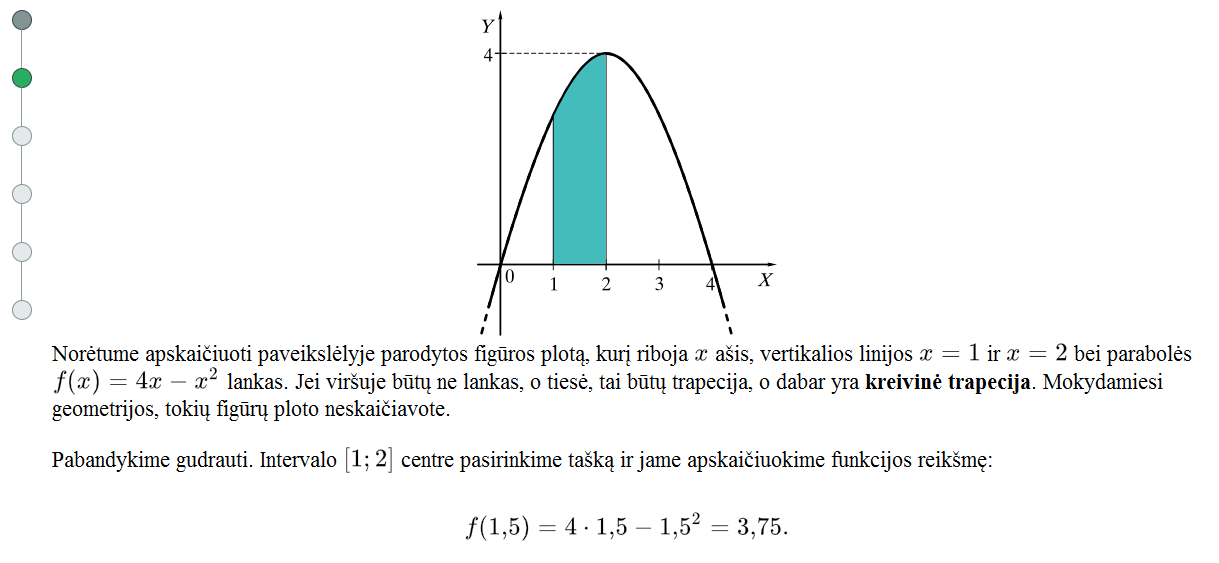
Mokinių klausiama, ar jie galėtų apytiksliai apskaičiuoti šios figūros plotą. Laukiamas atsakymas – šią kreivinę trapeciją reikia padalinti į gerai pažįstamas figūras (stačiakampius, trapecijas), kurių plotus apskaičiuoti nekiltų problemos. Tolesniame epizode nuosekliai paaiškinamas vienas iš būdų, kuriuo galima apytiksliai apskaičiuoti figūros plotą.
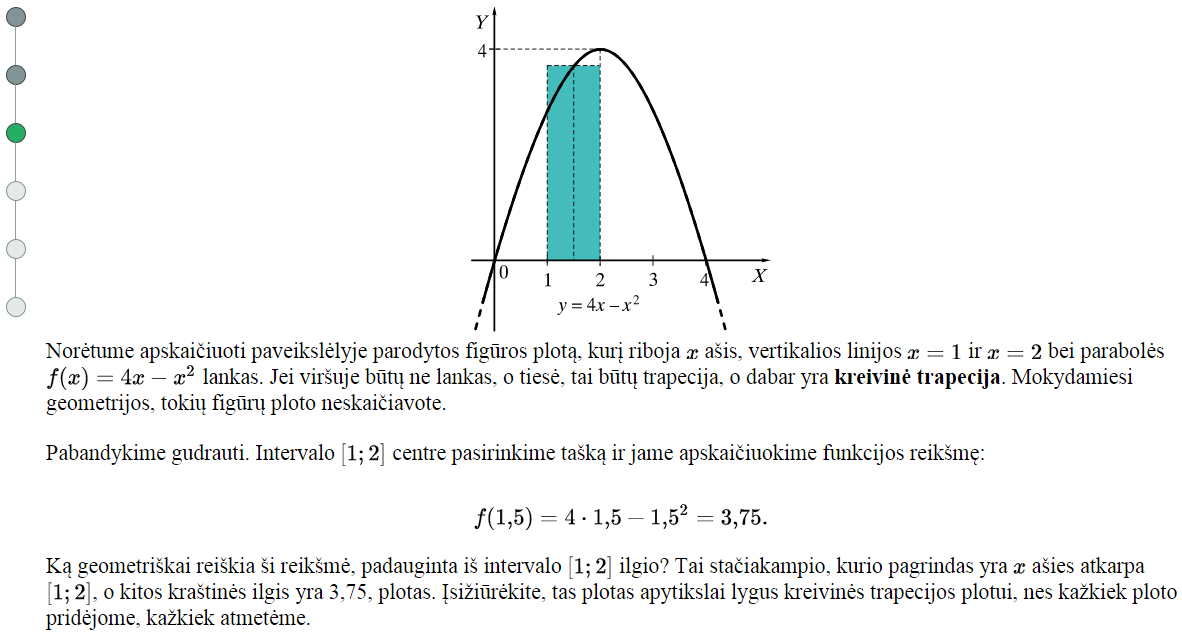
Mokinių klausiama, ką geometriškai reiškia ši reikšmė, padauginta iš intervalo [1;2] ilgio. Laukiamas atsakymas – stačiakampio plotą. Mokytojo komentarai ir demonstruojamas kitas epizodas. Mokytojo komentarai.
Mokinių klausiama, ar galima gauti tikslesnę reikšmę nei 3,75. Kokių veiksmų reikėtų imtis? Laukiamas atsakymas – kreivinės trapecijos plotą galime apskaičiuoti, ją pakeitę iš siaurų stačiakampių sudaryta figūra. Diskusija ir mokytojo komentarai.
Norint įsivaizduoti dalijimą, būtų paprasčiau papildomai naudoti interaktyvų Geogebra įrankį. Mokiniams trumpai paaiškinama, kaip nustatomos ribinės kreivinės trapecijos ploto reikšmės (leftrec – viršutinė riba; rightrec – apatinė). Mokiniams patiems leidžiama įsitikinti, jog didinant stačiakampių kiekį, artėjama prie vis tikslesnės kreivinės trapecijos ploto reikšmės.
2
Užduotis
Naudodami Geogebra įrankį:
Nustatykite stačiakampių skaičių 20. Pasižymėkite sąsiuvinyje ribines viršutines ir apatines plotų reikšmes (Left ir Right) ir suskaičiuokite tų reikšmių vidurkį.
Nustatykite stačiakampių skaičių 200. Pasižymėkite sąsiuvinyje ribines viršutines ir apatines plotų reikšmes (Left ir Right) ir suskaičiuokite tų reikšmių vidurkį.
Palyginkite (1) ir (2) vidurkių reikšmes. Pateikite išvadas.
3
Apibrėžtinis integralas
Apibrėžiama, ką vadinsime apibrėžtiniu integralu.
Paaiškinimui iliustruoti naudojama animuota Geogebra medžiaga:
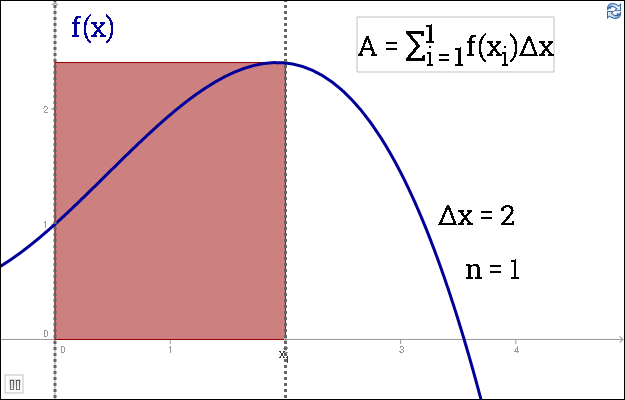
Demonstracija sustabdoma ties [latex]\triangle x = 2[/latex] ir [latex]n = 1[/latex]. Pakomentuojama suma. Plotas bus [latex]A = \triangle x \cdot f(x_1) = 2 \cdot f(2)[/latex]
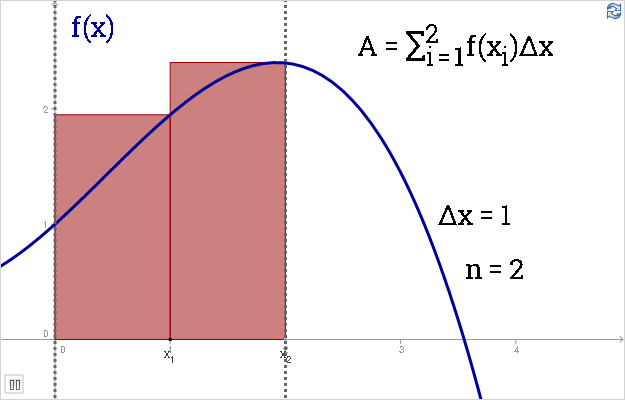
Demonstracija sustabdoma ties [latex]\triangle x = 1[/latex] ir [latex]n = 2[/latex]. Pakomentuojama suma. Plotas bus [latex]A = \triangle x \cdot f(x_1) + \triangle x \cdot f(x_2) = 1 \cdot f(1) + 1 \cdot f(2)[/latex]
Demonstracija sustabdoma ties [latex]\triangle x = 0.5[/latex] ir [latex]n = 4[/latex]. Pakomentuojama suma. Plotas bus [latex]A = \triangle x \cdot f(x_1) + \triangle x \cdot f(x_2) + \triangle x \cdot f(x_3) + \triangle x \cdot f(x_4)= 0.5 \cdot f(0.5) + 0.5 \cdot f(1) + 0.5 \cdot f(1.5) + 0.5 \cdot f(2)[/latex]
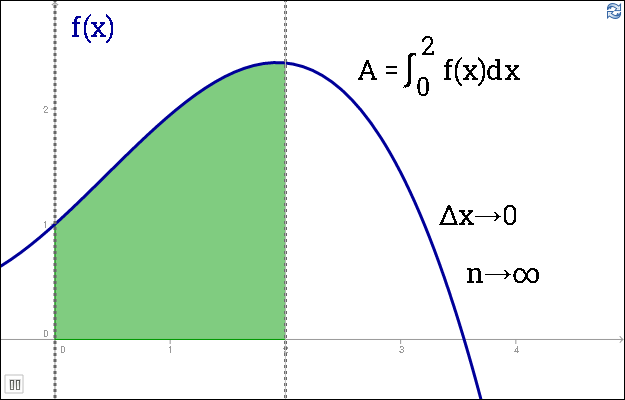
Neapibrėžtai didinamas dalijimas, ir animacija sustabdoma ties [latex]\triangle x \to 0[/latex] ir [latex]n \to \infty[/latex]. Pakomentuojama suma. Plotas bus [latex]A = \triangle x \cdot f(x_1) + \triangle x \cdot f(x_2) + \triangle x \cdot f(x_3) + \triangle x \cdot f(x_4) + \dots + \triangle x \cdot f(x_n) [/latex]
Akcentuojama, kad siaurus stačiakampius galime brėžti ir kitaip (2 užduotis), tačiau iš mažų stačiakampių sudaryta plotų sekos riba yra tapati.
Mokinių klausimai ir mokytojo komentarai.
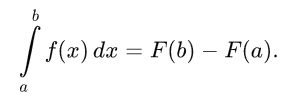
Jau žinome, kad kreivinės trapecijos plotas apskaičiuojamas naudojant apibrėžtinį integralą. Pristatoma Niutono–Leibnico formulė apibrėžtiniam integralui apskaičiuoti.
4
Niutono–Leibnico formulės taikymas
Pateikiamas aiškinimas, kaip apskaičiuoti kreivinės trapecijos plotą naudojant apibrėžtinį integralą ir Niutono–Leibnico formulę.
5
Apibrėžtinio integralo savybės.
Mokinių prašoma prisiminti (susirasti) neapibrėžtinio integralo savybes, kurios tinka ir apibrėžtiniam integralui.
Apibendrinimui atsakymai pateikiami tolesniuose epizoduose. Kiekvienas aptariamas.
6
Užduotis
Aukštesnysis lygis
Koordinačių plokštumoje pavaizduokite figūrą, apribotą nurodytomis tiesėmis ir kreivėmis [latex]y=0[/latex] [latex]y=2-x^2[/latex], [latex]x=0[/latex], [latex]x=1[/latex]. Brėžinį siūloma pasidaryti naudojantis dinaminės matematikos programa Geogebra. Kreivinės trapecijos plotui pavaizduoti naudojama įvesties komanda: Integralas Tarp[ <Funkcija>, <Funkcija>, <Pradžios x reikšmė>, <Galo x reikšmė> ]
Sudarykite apibrėžtinį integralą figūros plotui apskaičiuoti.
Apskaičiuokite figūros plotą ieškodami atitinkamų laiptuotų figūrų ploto ribos.
Apskaičiuokite apibrėžtinį integralą naudodami Niutono–Leibnico formulę.
Pagrindinis lygis
Koordinačių plokštumoje pavaizduokite figūrą, apribotą nurodytomis tiesėmis ir kreivėmis [latex]y=0[/latex] [latex]y=2-x[/latex], [latex]x=0[/latex], [latex]x=1[/latex]. Brėžinį siūloma pasidaryti naudojantis dinaminės matematikos programa Geogebra. Kreivinės trapecijos plotui pavaizduoti naudojama įvesties komanda: Integralas Tarp[ <Funkcija>, <Funkcija>, <Pradžios x reikšmė>, <Galo x reikšmė> ]
Apskaičiuokite gautos figūros plotą geometriškai.
Sudarykite apibrėžtinį integralą figūros plotui apskaičiuoti.
Apskaičiuokite apibrėžtinį integralą naudodami Niutono–Leibnico formulę.
Patenkinamas lygis
Koordinačių plokštumoje pavaizduokite figūrą, apribotą nurodytomis tiesėmis ir kreivėmis [latex]y=0[/latex] [latex]y=2x[/latex], [latex]x=0[/latex], [latex]x=1[/latex]. Brėžinį siūloma pasidaryti naudojantis dinaminės matematikos programa Geogebra.
Apskaičiuokite gautos figūros plotą geometriškai.
Sudarykite apibrėžtinį integralą figūros plotui apskaičiuoti.
Apskaičiuokite apibrėžtinį integralą naudodami Niutono–Leibnico formulę.
7
Sinusoidės ribojamas plotas
Pateikiama užduotis apskaičiuoti plotą, kurį riboja pirmojo periodo sinusoidė.
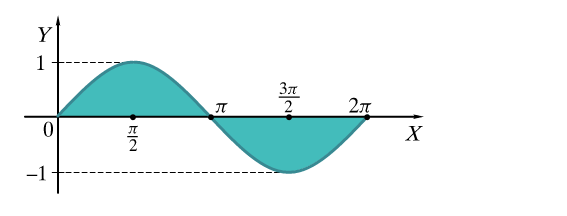
Brėžinys parodomas, tačiau sprendimas uždengiamas, ir prašoma mokinių sudaryti apibrėžtinį integralą nuspalvintos figūros plotui apskaičiuoti.
Prašoma sudaryti apibrėžtinį integralą figūros plotui ir jį apskaičiuoti. Tikėtinas rezultatas – bus gautas nulis. Klausiama, kodėl rezultatas gaunamas nulis.
Mokytojo komentarai. Paaiškinama ir akcentuojama padaryta klaida.
Jeigu intervale [latex][a; b][/latex] funkcija [latex]y = f(x) >0[/latex] , figūra bus virš [latex]O_x[/latex] ašies [latex]\int\limits_a^bf(x)\,dx=S[/latex].
Jeigu intervale [latex][a; b][/latex] funkcija [latex]y = f(x) <0[/latex] , figūra bus žemiau [latex]O_x[/latex] ašies [latex]\int\limits_a^bf(x)\,dx=-S[/latex].
Jeigu intervale [latex][a; b][/latex] funkcija [latex]y = f(x)[/latex], įgyja ir teigiamas, ir neigiamas reikšmes, figūra bus virš [latex]O_x[/latex] ašies ir po [latex]O_x[/latex] ašimi. Mūsų konkrečiu atveju taip ir yra. Intervale [latex][0;\pi][/latex] įgyja teigiamas reikšmes, o intervale [latex][\pi;2\pi][/latex] neigiamas. Abi figūrų dalys vienodos.
8
Integralo fizikinė prasmė
Primenama, kad [latex]\int{v(t)} = S(t)[/latex], nes [latex]S'(t) = v(t)[/latex]
9
Užduotis
Skiriamos pasirenkamojo atsakymo užduotys. Apibrėžtinis integralas, 7 epizodas.
10
Namų darbai
Skiriamos trumpo atsakymo užduotys. Apibrėžtinis integralas, 8 epizodas.
Pagrindinio (II) ir Aukštesniojo (III) lygio
Duota funkcija [latex]y = f(x) = {1 \over{2}} x^2, x \in [0;4][/latex]
- Taškais [latex]x_1, x_2, x_3, x_4[/latex] padaliję nurodytą intervalą į keturis to paties ilgio [latex]\triangle x[/latex] intervalus, apskaičiuokite sumą
[latex]S_4 = \triangle x \cdot f(x_1) + \triangle x \cdot f(x_2) + \triangle x \cdot f(x_3) + \triangle x \cdot f(x_4)[/latex].
- Pavaizduokite funkciją [latex]y = f(x)[/latex] ir laiptuotą figūrą [latex]S_4[/latex].
- Apskaičiuokite figūros plotą naudodami Niutono–Leibnico formulę.
Atliekant užduotį siūloma naudojantis dinaminės matematikos programa Geogebra.
Aukštesnio (III) lygio
Jauna šeima Petriukas ir Onytė ieško sklypo kaimo turizmo sodybai įrengti. Internete rado skelbimą, jog parduodamas žemės sklypas prie upelio. Informacijoje apie sklypą yra pridėtas brėžinys (duomenys pateikti metrais AO = 200 m, BC = 300 m). Pardavėjo nurodyta sklypo kaina 120 000 eurų.
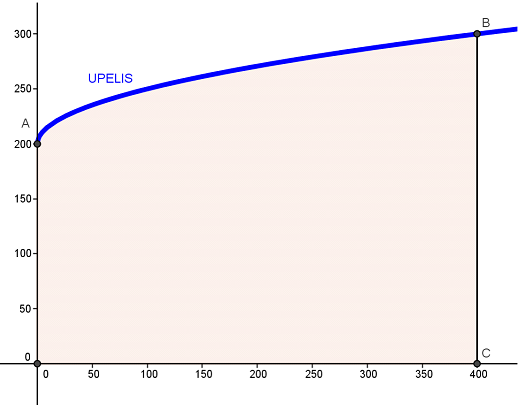
Petriukas ir Onytė nusprendė rimtai panagrinėti pasiūlymą.
Žinodami, jog sklypo ribose upelio vingis primena funkcijos [latex]y = U(x) = a\sqrt{x} + b[/latex] grafiką, parodykite, kad [latex]y = U(x) = 5\sqrt{x} + 200[/latex]
Sudarykite apibrėžtinį integralą sklypo plotui apskaičiuoti;
Apskaičiuokite sklypo plotą vieno aro tikslumu;
Petriukas ir Onytė sužinojo, jog šio sklypo 1 aro rinkos kaina yra 100 eurų. Apskaičiuokite viso sklypo rinkos kainą. Kaip manote, kiek realu nusiderėti?
Brėžinį siūloma pasidaryti naudojantis dinaminės matematikos programa Geogebra.
11
Pasiekimų ir pažangos vertinimas
Pamokoje naudojamas kaupiamasis vertinimas, kuris taikomas vertinant:
- teisingus mokinių atsakymus į klausimus;
- savarankiško darbo užduotis;
- mokėjimą pagrįsti išsakytą nuomonę;
- aktyvumą ir iniciatyvumą pamokoje;
- pagalbą draugui;
- mokymosi pažangą.
Namų darbų užduotis pristatoma ir aptariama kitos pamokos pradžioje. Išsamiausi atsakymai ir pristatymai vertinami kaupiamaisiais balais.
12
Apibendrinimas
Pamokos refleksijai skiriamos kelios minutės. Mokiniai peržvelgia savo užrašus, prisimena veiklas ir pildo pasiūlytą lentelę.
Mokytojas paprašo perskaityti savo refleksijas, trumpai pakomentuoja jas, patardamas, kaip ir į ką turėtų atkreipti dėmesį mokiniai, siekdami geresnių rezultatų.