Aukštesnysis lygis
„Pasirenkamojo atsakymo užduotys. Sinuso funkcija“ (MO rinkinio 8 kadras). Renkasi A lygį. Sistema tikrina, mokiniai pasitikrina ir nagrinėja neteisingus atsakymus. Mokytojo pagalba ir komentarai.
Motyvuojantis įvadas
Primenamas sinuso apibrėžimas.
Statinio, esančio prieš kampą, ilgio santykis su įžambinės ilgiu yra to kampo sinusas:
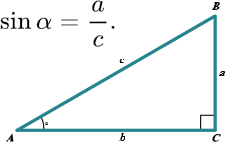
Keliamas klausimas: kaip, keičiant sinuso kampo dydį, pamatyti sinuso kampo reikšmes? Laukiamas atsakymas – trikampyje arba vienetiniame apskritime stebint statinio prieš kampą dydį.
Esant poreikiui, pakartoti sin, cos ir tg apibrėžimus, galima naudoti kartojimo testą.
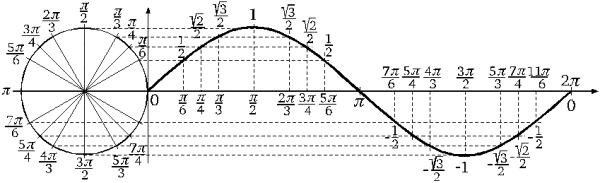
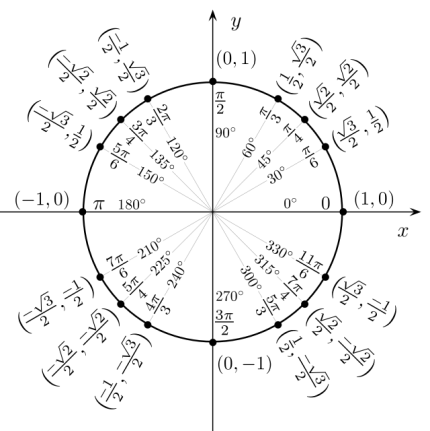
Dinaminiu paveikslėliu demonstruojama, kaip vienetiniame apskritime stebimos sinuso reikšmes. Mokinių klausiama, kada sinuso reikšmė lygi 1; 0; -1. Mokytojo ir mokinių komentarai.
Mokinių klausiama, kaip koordinačių plokštumoje galėtume nubrėžti sinuso reikšmių y priklausomybės nuo kampo x grafiką. Laukiamas atsakymas – ordinatėje atidėti y reikšmes, o abscisių ašyje atidėti kampo x dydžio reikšmes.
Parodoma, kaip vaizdžiai sinuso reikšmių kitimą parodo grafikas – sinusoidė.
Užduotys
Mokiniai naudojasi parengtu įrankiu, 9 kadras – „Sinuso funkcija“. Prašoma nagrinėti ir užsirašyti sinuso funkcijos savybes:
-
Apibrėžimo ir reikšmių sritis;
Didžiausią ir mažiausią reikšmes;
Reikšmes su kuriomis įgyja didžiausią ir mažiausią reikšmes;
Mažiausią teigiamą periodą;
Lyginumą;
x reikšmių intervalus, kuriuose funkcijos reikšmės yra teigiamos ir neigiamos;
x reikšmių intervalus, kuriuose funkcijos reikšmės didėja ir mažėja.
Mokytojo komentarai ir pagalba. Siūloma papildomai leisti mokiniams naudotis šiais paveikslėliais:
Motyvuojantis intarpas
Sinusiniai virpesiai.
-
Mokiniams paaiškinama, kad sinusiniai virpesiai apibūdinami dviem susijusiais parametrais – dažniu (angl. frequency) ir bangos ilgiu. Demonstruojamas įvairių bangų spektras.
Paaiškinama, kas yra vieno herco dažnis, ir kaip jis siejasi su sinusoidės periodu. Trumpa diskusija. Mokytojo komentarai.
Akcentuojama:
-
Radijo bangos – elektromagnetinės bangos, kurių bangos ilgis didesnis nei 1 mm.
Radijo bangos dažnis – tai ciklų skaičius per vieną sekundę. Kuo didesnis vieno ciklo laikas, tuo didesnis bangos ilgis, ir tuo žemesnis dažnis. Ir atvirkščiai. Dažnis matuojamas hercais (Hz). Kadangi radijo bangos dažnis yra labai didelis, jis paprastai matuojamas tūkstančiais hercų (kilohercais, kHz) ir milijonais hercų (megahercais, MHz).
Bangos ilgis – atstumas nuo vienos iki kitos bangos viršūnės (t.y. dviejų vienodos fazės taškų). Tai yra atstumas, kurį nukeliauja banga, atlikdama vieną svyravimą. Bangos ilgis visada matuojamas metrais. Bangos ilgį galime apskaičiuoti žinodami šviesos greitį (300 000 km/s) ir bangos dažnį.
Motyvuojantis intarpas
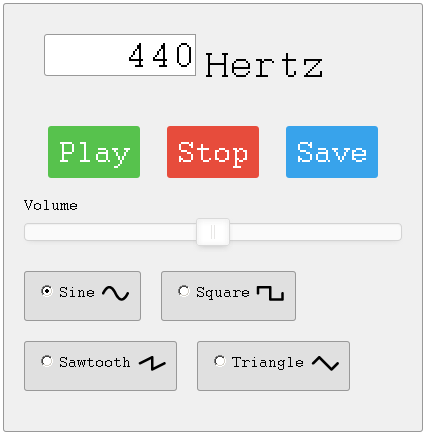
Garso bangų generatorius internete
Motyvuojantis intarpas
Tono generatoriumi yra vibruojama metalinė plokštė, ir ant jos pilamos smulkios kruopelės. Keičiant virpesių dažnį, stebimas kruopelių „šokis“. Originalus Resonance Experiment! Žiūrėdami originalą BŪTINAI įsitikinkite, kad garso sistema nutildyta.
„Armonikos“ transformacija. Dažnis
Mokinių klausiama, kaip keičiasi grafikas, funkcijoje keičiant koeficientą a. Demostruojamas aiškinimas, kaip, keičiantis koeficiento a reikšmei, vyksta sinusoidės „suspaudimas“ ir „ištempimas“.
Galima paminėti, kad šis koeficientas fizikoje nurodo bangos dažnį, kitaip sakant, nurodo sinusoidės bangų skaičių periode 2π. Periodas yra atstumas (arba laikas), per kurį realizuojama viena sinusoidės banga (ciklas). Mokinių klausiama, kokia yra koeficiento a įtaka sinusoidės periodui ir reikšmių sričiai. Laukiamas atsakymas – sinusoidės sinax periodas T apskaičiuojamas taip: T = 2π/|a|, o reikšmių sritis nekinta.
Akcentuojama, jog didesnė a reikšmė suteikia didesnį dažnį, bet mažesnį periodą.
Nurodoma pasiskaityti Wiki.
„Spyruoklės transformacija. Amplitudė
Akcentuojama, jog fizikoje sinusoidės kreivė natūraliai aktuali nagrinėjant bangas. Kai bangos turi daugiau energijos, jos kyla aukštyn ir žemyn energingiau. Sakoma, kad jos turi didesnę amplitudę.
Mokinių klausiama, kokia yra koeficiento a įtaka sinusoidės periodui ir reikšmių sričiai. Laukiamas atsakymas – periodas nesikeičia, o minimali ir maksimali reikšmės yra dauginamos iš koeficiento a reikšmės.
Nurodoma pasiskaityt Wiki.
Naudojantis Geogebra sukurtu įrankiu graphof y = a sin (bx) + c mokiniams demonstruojamas vertikalus sinusoidės postūmis per dydį c.
Mokinių klausiama, kokia yra koeficiento c įtaka sinusoidės periodui ir reikšmių sričiai.
Laukiamas atsakymas, jog periodas nesikeičia, o minimali reikšmė apskaičiuojama -1+c, maksimali reikšmė apskaičiuojama 1+c.
Užduotis
Pagrindinis lygis
„Pasirenkamojo atsakymo užduotys. Sinuso funkcija“ (MO rinkinio 8 kadras). Renkasi A lygį. Sistema tikrina, mokiniai pasitikrina ir nagrinėja neteisingus atsakymus. Mokytojo pagalba ir komentarai.
Patenkinamas lygis
„Pasirenkamojo atsakymo užduotys. Sinuso funkcija“ (MO rinkinio 8 kadras). Renkasi B lygį. Sistema tikrina, mokiniai pasitikrina ir nagrinėja neteisingus atsakymus. Mokytojo pagalba ir komentarai.
Namų darbai
Aukštesnysis lygis
„Trumpo atsakymo užduotys. Sinuso funkcija“ (MO rinkinio 9 kadras). Renkasi A lygį. Sistema tikrina, mokiniai pasitikrina ir nagrinėja neteisingus atsakymus. Mokytojo pagalba ir komentarai.
Pagrindinis lygis
„Trumpo atsakymo užduotys. Sinuso funkcija“ (MO rinkinio 9 kadras). Renkasi A lygį. Sistema tikrina, mokiniai pasitikrina ir nagrinėja neteisingus atsakymus. Mokytojo pagalba ir komentarai.
Patenkinamas lygis
„Trumpo atsakymo užduotys. Sinuso funkcija“ (MO rinkinio 9 kadras). Renkasi B lygį. Sistema tikrina, mokiniai pasitikrina ir nagrinėja neteisingus atsakymus. Mokytojo pagalba ir komentarai.
Pasiekimų ir pažangos vertinimas
Pamokoje naudojamas kaupiamasis vertinimas, kuris taikomas vertinant:
- teisingus mokinių atsakymus į klausimus;
- savarankiško darbo užduotis;
- mokėjimą pagrįsti išsakytą nuomonę;
- aktyvumą ir iniciatyvumą pamokoje;
- pagalbą draugui;
- mokymosi pažangą.
Namų darbų užduotis pristatoma ir aptariama kitos pamokos pradžioje. Išsamiausi atsakymai ir pristatymai vertinami kaupiamaisiais balais.
Apibendrinimas
Pamokos apibendrinimui galima naudoti Geogebra įrankį y = a sin (bx) + c akcentuojant koeficientų a, b ir c įtaką sinusoidės grafikui.
Pamokos refleksijai skiriamos kelios minutės. Mokiniai peržvelgia savo užrašus, prisimena veiklas ir pildo pasiūlytą lentelę.
Mokytojas paprašo perskaityti savo refleksijas, trumpai pakomentuoja jas, patardamas, kaip ir į ką mokiniai turėtų atkreipti dėmesį, siekdami geresnių rezultatų.
